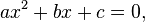Topic:-quadratic equation
A quadratic equation is equation is a polynomial equation of the second degree. The general form is
The constants a, b, and c, are called respectively, the quadratic coefficient, the linear coefficient and the constant term or free term. Quadratic comes from quadratus, which is the Latin word for "square."
This math help gives a example as well.
Question:-
A quadratic equation is equation is a polynomial equation of the second degree. The general form is
The constants a, b, and c, are called respectively, the quadratic coefficient, the linear coefficient and the constant term or free term. Quadratic comes from quadratus, which is the Latin word for "square."
This math help gives a example as well.
Question:-
x2-12x+27 x+9
--------- * -------
x2-81 3-x
Answer:-
Let's start with simplifying the quadratic expression
x2-12x+27
x2-3x-9x+27
x(x+3)-9(x-3)
(x-3)(x-9)
Let's substitute it back in the given equation
(x-3)(x-9) x+9
--------- * -------
x2-81 3-x
(x-3)(x-9) x+9
---------- * -------
(x+9)(x-9) 3-x
Cancel the similar terms on numerator with denominator
We get
x-3
-------
3-x
We can write 3-x as -(x-3)
So x-3
------- = -1
-(x-3)
So -1 is the answer.