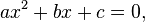Introduction to Linear Equation:
In this section let me help you go though on what is a linear equation. linear equation is an algebraic equation in which each term is either a constant or the product of a constant and (the first power of) a single variable.
Linear equations can have one or more variables. Linear equations occur with great regularity in applied mathematics. While they arise quite naturally when modeling many phenomena, they are particularly useful since many non-linear equations may be reduced to linear equations by assuming that quantities of interest vary to only a small extent from some "background" state.
Solving One-step Linear Equations
solve x + 6 = –3
We want to get "x" on one side of the equal sign, and some number on the other side. Since we want x on the one side, this means that we don’t need the "plus six" that's currently on the same side as the x. Here 6 is added to the x, hence we need to subtract to get rid of it. That is, we need to subtract 6 from the x in order to "undo" having added a 6 to it. This could also help us on how to graph linear equations
Solution:
x + 6 = -3
-6 = -6
x =-9
The value of x = -9
In this section let me help you go though on what is a linear equation. linear equation is an algebraic equation in which each term is either a constant or the product of a constant and (the first power of) a single variable.
Linear equations can have one or more variables. Linear equations occur with great regularity in applied mathematics. While they arise quite naturally when modeling many phenomena, they are particularly useful since many non-linear equations may be reduced to linear equations by assuming that quantities of interest vary to only a small extent from some "background" state.
Solving One-step Linear Equations
solve x + 6 = –3
We want to get "x" on one side of the equal sign, and some number on the other side. Since we want x on the one side, this means that we don’t need the "plus six" that's currently on the same side as the x. Here 6 is added to the x, hence we need to subtract to get rid of it. That is, we need to subtract 6 from the x in order to "undo" having added a 6 to it. This could also help us on how to graph linear equations
Solution:
x + 6 = -3
-6 = -6
x =-9
The value of x = -9


 Mr.R's age is 7x years.
Mr.R's age is 7x years. 7x + 10 = 3x + 30
7x + 10 = 3x + 30 5 = 35 years
5 = 35 years